
I’m trying something new with this post. I’m going to try to keep this short and sweet. Get in and out quick. Get right to the point. No more long-winded, drawn out, over explained blog posts. (I’m not off to a good start am I?)

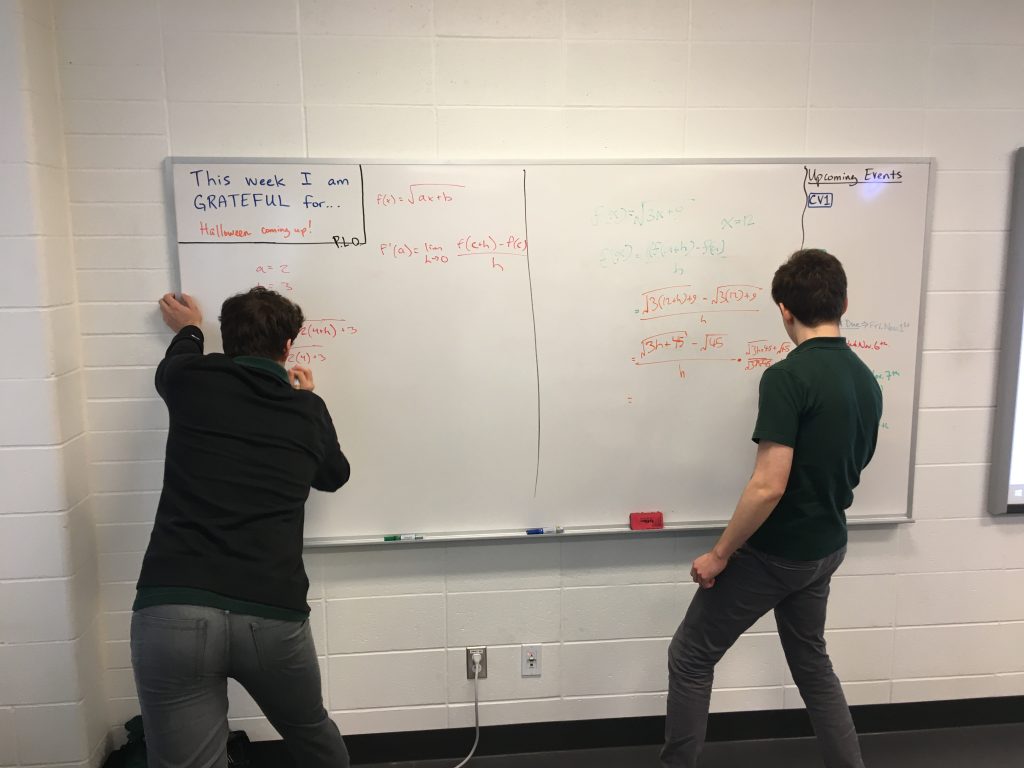
I’ve been trying something in my calculus class lately. It involves VNPS. This stands for “Vertical Non-Permanent Surface” and the goal is to get students up on their feet working working on a surface that easily erases, which means they don’t have to be afraid to make mistakes (see image below). I’ve had students do VNPS individually sometimes and in groups other times. When I use groups I have the students draw cards to determine their partners. I do this based on the recommendations of Peter Liljedahl in order to ensure fairness, that students work with others they wouldn’t normally choose to work with, and mainly to avoid the constant complaints 🙂

VNPS is nothing new. Many math teachers all over the world are using it in their classrooms. So how have I been using it specifically? (FINALLY THIS GUY GETS TO THE POINT! So much for short and sweet!) I’ve been giving my students the skeleton of problem and then I have them choose their own values for the constants and exponents I’ve indicated. The image below is an example of this.

This way each student/group has their own unique problem, whose answer will most likely not be “nice”. Interestingly enough, the feedback from my students has been that they like having to work through problems with “not nice” answers, unlike the problems in their textbooks.
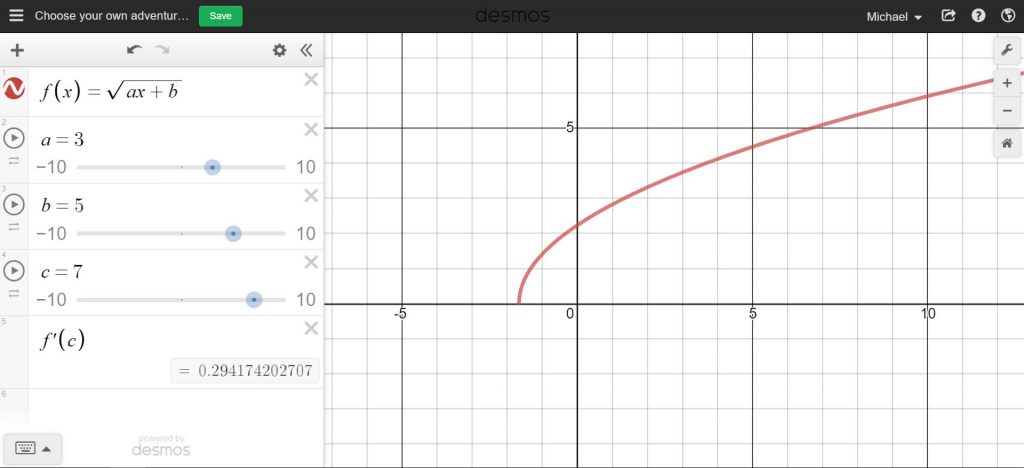
So how do I check their answers? I’m so glad you asked. Desmos of course! I type in the equation I gave the students with the constants a, b, c, etc. and Desmos allows me to create sliders for these constants (careful not to use certain letters that already have pre-programmed values like e and i). When a student wants their answer checked, I simply input their a, b, c, etc. values and Desmos tells me the answer immediately (see image below). Here is the Desmos graph I used if you’d like to play with the sliders.
Here are a few shots of what my students came up with.

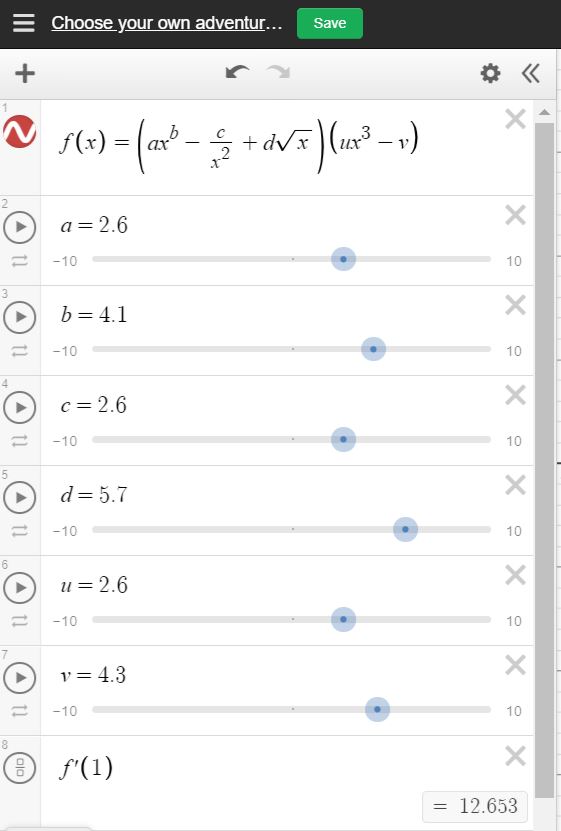
Another example of when I used this was during a product rule lesson. See image below.

I realize these are 2 calculus examples but this can work in any math class. Off the top of my head…
- Grade 9 – Have students choose 2 random points and determine the equation of the line passing through them. Set up Desmos to calculate the slope and y-intercept automatically.
- Grade 10/11 – Have each student solve their own intersection of a parabola and a line problem. They choose their own a, b, c values for a quadratic in standard form and the slope and y-intercept of the line, then solve the system. Have Desmos graph the two functions and then click on the POI’s. (You could also start the quadratic in factored or vertex form to add a challenge. Now that I think about it, this is probably better because it’ll be easier to ensure that the system has solutions.)
- Grade 12 Advanced Functions – Set up a general polynomial in factored form, with some factors having powers or 2 or 3, then have them choose their zeros and sketch their unique graph. Have Desmos graph their function and compare.
Ok, I think I’ll stop my rambling here. It wasn’t exact short and sweet, but at least there were pictures 🙂
If you’re interested, I have also blogged in the past about other things I’ve tried. Here are a few links:
- “Are you ready for calculus?” – A diagnostic and feedback approach to starting the MCV4U course.
- “Math is Fun Fridays” – An explanation of how I try to make Fridays a little more fun and a link to the activities I use.
- “The I Need Help Zone” – Something I tried that went fairly well.
- “Today I’m Grateful For” – A blog about what I started doing in my classroom last year.
Lastly, I’m going to call on my fellow Cohort 21 mathies to share something they’ve tried in the last year or two, no matter how small. Either leave a comment below or write your own blog post about it! Let’s all help each other out by highlighting and sharing our successes.
@sletham @mmurray @ldickinson @psenior @jgravel @mhodal @elee @hjepson

Images courtesy of –> https://www.tes.com/lessons/IA90Bt0VyO23CA/8th-math-review

Great idea Mike! I have been using VNPS a lot this year, but had not thought if trying this out! Now I am going to give it a go with my grade 9 and 10s! I will let you know how it turns out.
This year one of the things I am trying is to have more student centred investigations, to discover patterns that lead to math rules and laws. For example, this week my grade 9’s carried out an exponent law investigation in randomly assigned pairs. Though some students found it challenging to get started (didn’t want to work with their partners, don’t like to be in the pit of struggle, etc.), most came around once they got into it. What I loved the most, was that some of the weakest students got the most out of the experience! They really talked it through with their partners until they came up with something that made sense. I overheard one pair discussing it afterwards, and one girl exclaimed how proud she was of herself and her partner for completing the investigation together and coming to the right conclusions! I WAS SO HAPPY TO HEAR THIS! They were excited that they had learned not only the math concepts, but had problem solved successfully! WOW!
I love this idea but I’ve never been brave enough to try it myself! The furthest I’ve gone in letting students discover concepts by playing around is using different teacher.desmos.com activities, i.e. exploring what changing the a, h, k values of a parabola in vertex form does to the graph.
I’m so glad your students had a positive experience with this and I hope the next one goes even better! I’d love to hear more specifics this weekend at the next F2F. See you then!
Your pictures and approach here remind me of @ckirsh recent podcast on deskless classroom – that just adjusting the “third teacher” in the room can lead to a deeper culture of language – in this case the language of math.
I wonder what our other math teachers think about these approaches?
Garth.
Thanks @gnichols ! I haven’t listened to that one yet. I know what I’m doing on the way home 🙂
While I cannot profess to have any understanding of the math you’re showing here, I love that you’ve included examples that other math teachers can transfer into their practice. Short and sweet? Verdict’s out on that one. 😉 Regardless, this post has a tonne of useful resources in it, modelling yet another great use of this platform!
Thanks Jess! I’ve stolen lots of ideas from non-math teachers over the years so I’m happy to hear that a teacher from another discipline found parts of my sharing useful. Thank you for taking the time to read and comment!
@mmoore,
I love the term, “not nice answers” as somehow being in opposition to the textbook. I find, developmentally, that the more you can create “rebel” situations in upper adolescence, a sense of getting away with something (whether it actually is NEW or not!).
The only thing I’m missing here is how this connects to the Mathematical Processing skills, and any relevant or meaningful connection to the real world. I’m all for the importance of Mathematical mindsets and problem solving for the sake of it, but can’t Math teachers do both!
Eric
It’s coming @edaigle … we need to learn to walk before we run. Even in calculus we’re still learning our “ABC’s”, which require practice without context. The context coming soon, however, for example we’ll be asking questions like “given a soda can must hold 355 mL of liquid, redesign the can so it uses the least amount of material as possible”.
I love your idea of rebelling. I never thought of it in this context but I think you’re right as to why they enjoy the messy answers.
Thanks for the feedback! See you Saturday!
“Not nice answers”, VNPS, short blog posts that aren’t – Mike, you are always a rebel!
I love how you mention that you have “stolen lots of ideas from non-math teachers”. Taking the ideas of others and making them your own is not only a sincere form of flattery but also a natural way to learn to do something. I think there are many ideas here that others could steal from you:
– allowing students to both differentiate and drive part of their learning by selecting their own values and constants — we could all do this: give students more opportunity for input
– utilizing “the third teacher” as @gnichols mentioned – the classroom environment can have such a huge impact on how we function in a space. Like you our french teachers have found that students write far more and take greater risks with vocabulary when writing collaboratively on large whiteboards that everyone can see and our grade 2 teacher has found that what gets written there is more “ours” and so students tend to add more to one another’s ideas
– the use of technology (desmos) to quickly and easily evaluate student work done in an analogue manner – the technology serves a specific purpose and allows you to give students pretty immediate feedback
– even as an introvert, collaborative learning, in my mind, almost always trumps individual public displays of learning – having the opportunity to talk through what to do next and what makes sense deepens understanding
Thanks for not limiting this to being just a short post – all your pictures and explanations really helped me to understand your process (and I haven’t thought about math like this since 1985!)